I'm following the online Harvard CS50 course and I'm making my notes public!

Lecture

Prof Malan wants to take attendance. He could simply count everyone in the room, but he proposes a better solution. Everyone in the room stands up and has the value 1. Now everyone partners with another person. One of them adds up the value of the other person to their own value (so 2) and the other person sits down. This process gets repeated until there's only 1 person standing. This person holds the value that corresponds with the total attendance.

This is similar to what prof Malan did in the first lesson when he tore up the phone book to demonstrate an algorithm to search for a person. You don't go over every name, but you divide the collection in half (tearing up the phone book). You keep repeating the process until you're left with only 1 page.

This means that, if the phone book would double in size, you'd only need 1 more step. If you'd go over every name from start to end, your work would double. So even in the data set increases, the time to search stays almost the same.

Linear search

Something important to remember about array, is that the bytes are stored back to back to back in the computer's memory. It's contiguous.

If you have an array that holds [1,5,10,20,50,100,500] you can easily see what the values are. However, a computer doesn't have this birds eye view. A computer can only look at number at a time to find a specific value.

You can imagine it as a series of gym lockers. They have numbers (zero-based indexes), but the doors are locked so you can't see the values. You have to open them one at a time to see the content.

Imagine you're standing for 7 lockers. One of the lockers contains 50 dollars. The first way to look for the 50 dollars, is to open up the lockers one at a time (from right to left or from left to right). This is your only option if the values are unsorted.

Linear search (pseudo code)

• For each door from left to right
  • If 50 is behind door
    • Return true
• return false (50 can't be found)

Or more concrete:

• For i from 0 to n-1
  • If 50 is behind doors[i]
    • Return true
• return false

Binary Search

However, if the dollar bills are ordered, you can simply open up the middle one and divide the problem in half. If you find a 20 there, you know that you can skip all the lockers on the left side. With the remaining lockers, you take the middle one as well. So you repeat the process.

Pseudo code

• if no doors left
  • return false
• If 50 is behind middle door
  • return true
• else if 50 < middle door
  • search left half
• else if 50 > middle door
  • search right half

Or more concrete:

• If no doors left
  • return false
• If 50 is behind doors[middle]
  • return true
• Else if 50 < doors[middle]
  • Search doors[0] through doors[middle-1]
• Else if 50 > doors[middle]
  • Search doors[middle+1] through doors[n-1]

Running time

The green line represents the time it takes when using binary search. When the size doubles, that's just 1 more step (1 more loop).

The red line is linear search.

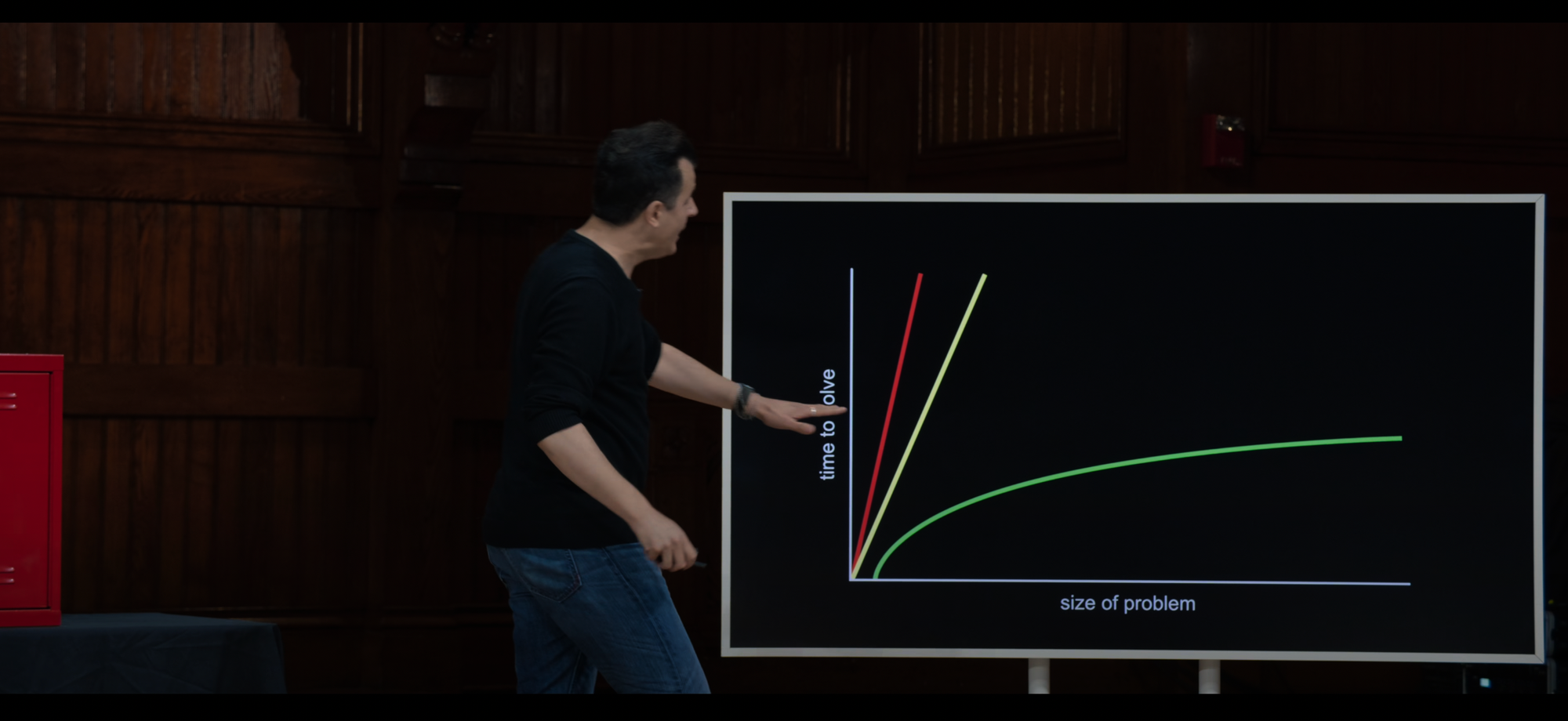
Red line: n
Green line: log2n

When we talk about the efficiency of an algorithm, we talk about "on the order of". The lower levels details don't matter that much.

Red line: O(n)
Green line O(log2n)

Computer scientist also tend to throw away the absolute numbers

Red line: O(n)
Green line: O(log n)

The 'O' is called big O notation

• O(n²)
• O(n log n)
• O(n)
• O(log n)
• O(1)

Big O of n means that it takes linear time (from left to right. The amount of steps is takes is on the order of n)

Big O represents the worst case of steps it may take you. So if you're looking for John Harvard in a phone book that holds the contact information for 2000 people, you'd have to do 2000 steps (worst case)

O(n²) would for example be if everyone in the room shook hands with eachother. It would take you n² handshakes.

O(1) means that it's a constant amount of steps. It could be 1, 1000, 2000, etc. No matter how big the data set is, the amount of steps is constant. For example, if you ask everyone in the room to stand up, that's a constant time algorithm. If you have 5 people, it takes 1 step (everyone stands up at the same time). If there are 5000 people, it still takes 1 step.

O(log n) is binary search because you keep dividing in half. Log n means number of times n must be divided by the base to get 1.

Big O refers to the worst case (upper bound), the maximum amount of steps it can take. But we can also talk about a best case scenario, because even with linear search sometimes you get lucky. We use the omega sign (Ω) to talk about this.

• Ω(n²)
• Ω(n log n)
• Ω(n)
• Ω(log n)
• Ω(1)

So by that logic, if you search 7 lockers and you get lucky, it would take you 1 step. Omega of 1.

Binary search: in the best case it would take you 1 because it could be right in the middle.

But if you want to take attendance and you count everyone in the room, even in the best case it would always take you n steps. There is no way to "get lucky" here.

When Big O and Omega happen to be the same, we use Theta notation Θ.

Big O notation describes the upper bound or worst-case scenario of an algorithm. Omega notation (Ω) describes the lower bound or best-case scenario. When they're the same (for example when counting all the people in a room), we use Theta notation (Θ) which means that the upper and lower bounds are the same.

• Θ(n) for example when you count all the people in a room

Search.c

Numbers

If you want to implement linear search in C, you could do it like this if you want to look for a number in an array of number:

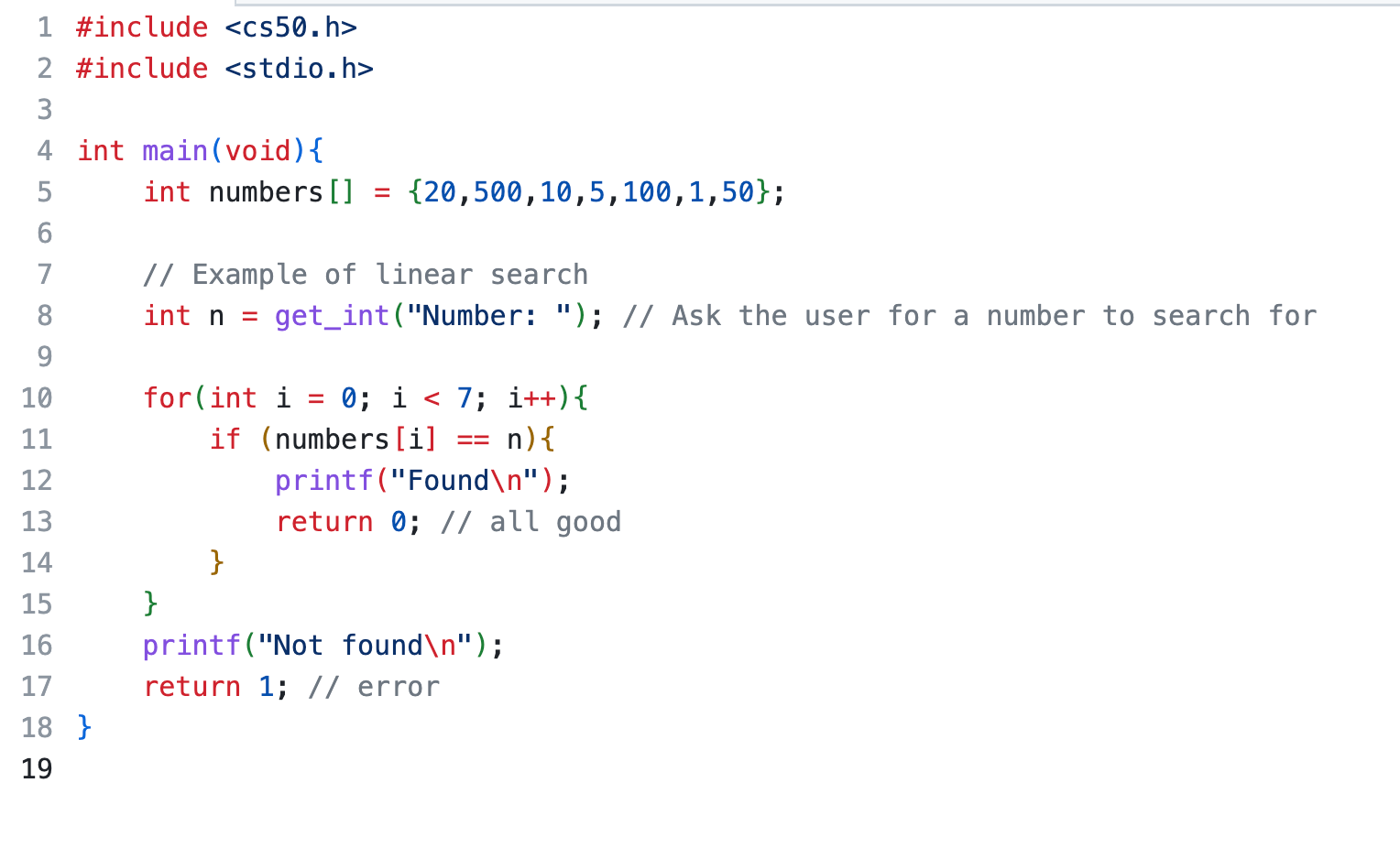
We use 'return 0' to signal that everything is good (success) and to terminate the program (so that it doesn't print out the "not found")

Strings

If you want to compare strings, you can't use something like this:

string s = "battleship" 
if (strings[i] == s)

Instead, you use strcmp(). If this function returns 0, that means that the strings are the same. To work with this, you'll need to include the header file string.h

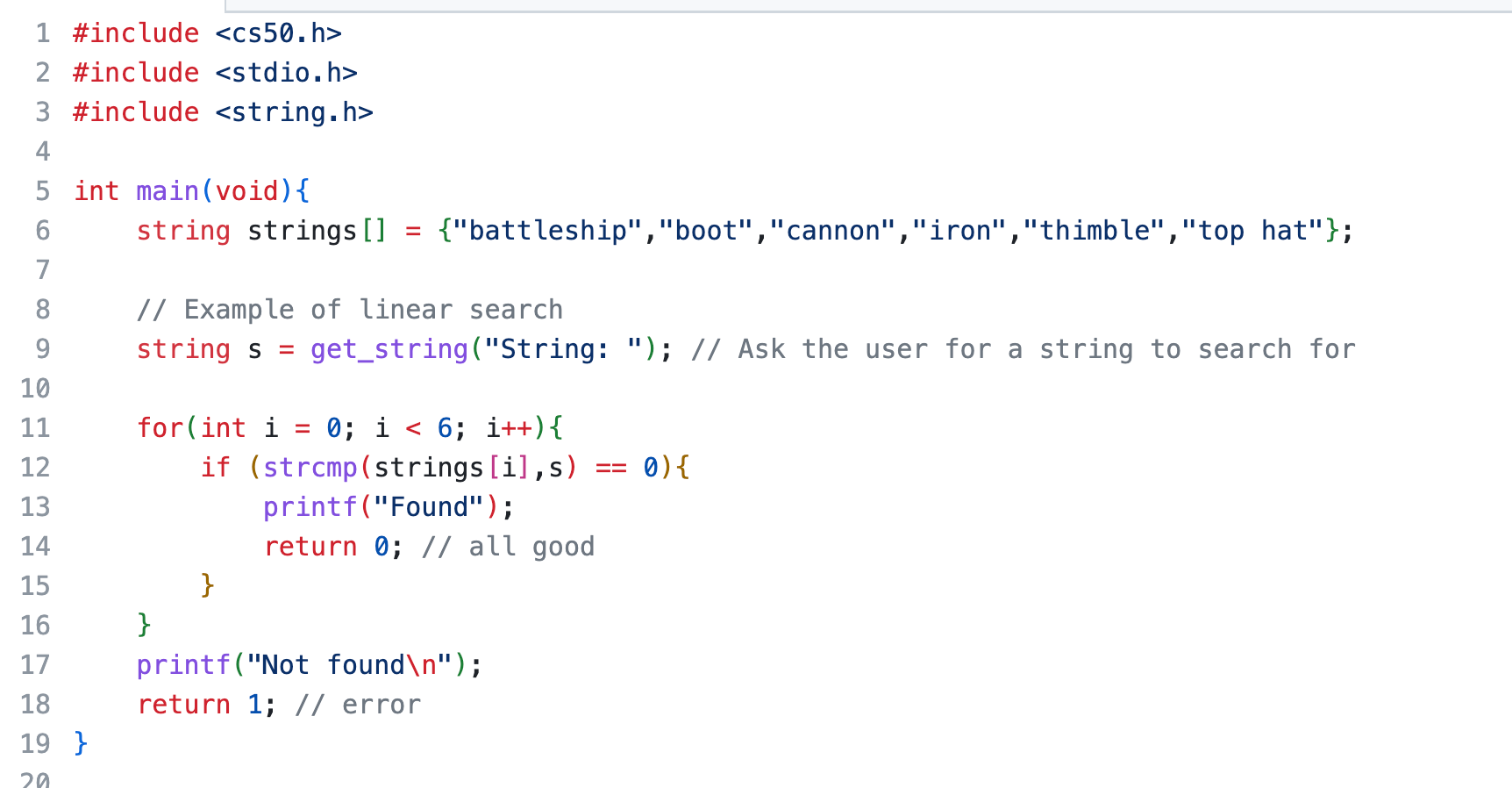
How strcmp works, is that it checks for ASCIIbetical order. So if the strings are the same, there is no difference in the order. So if you compare a, it's gonna compare 65 to another value.

Phonebook.c

It's best to store phone numbers as strings. If you don't to math on a number (like a phone number), you should store it as a string. This way you also don't risk overflow, and you can use special characters like plusses and dashes.

We want to create a simple phonebook program. The user enters a name, and the program returns the phone number.

But how do we store both the name and the matching phone number? This is a great opportunity to create our own data structures.

Let's create a data type 'Person' that holds a name and a number. We use a struct for this.

typedef struct{
  string name;
  string number;
} person;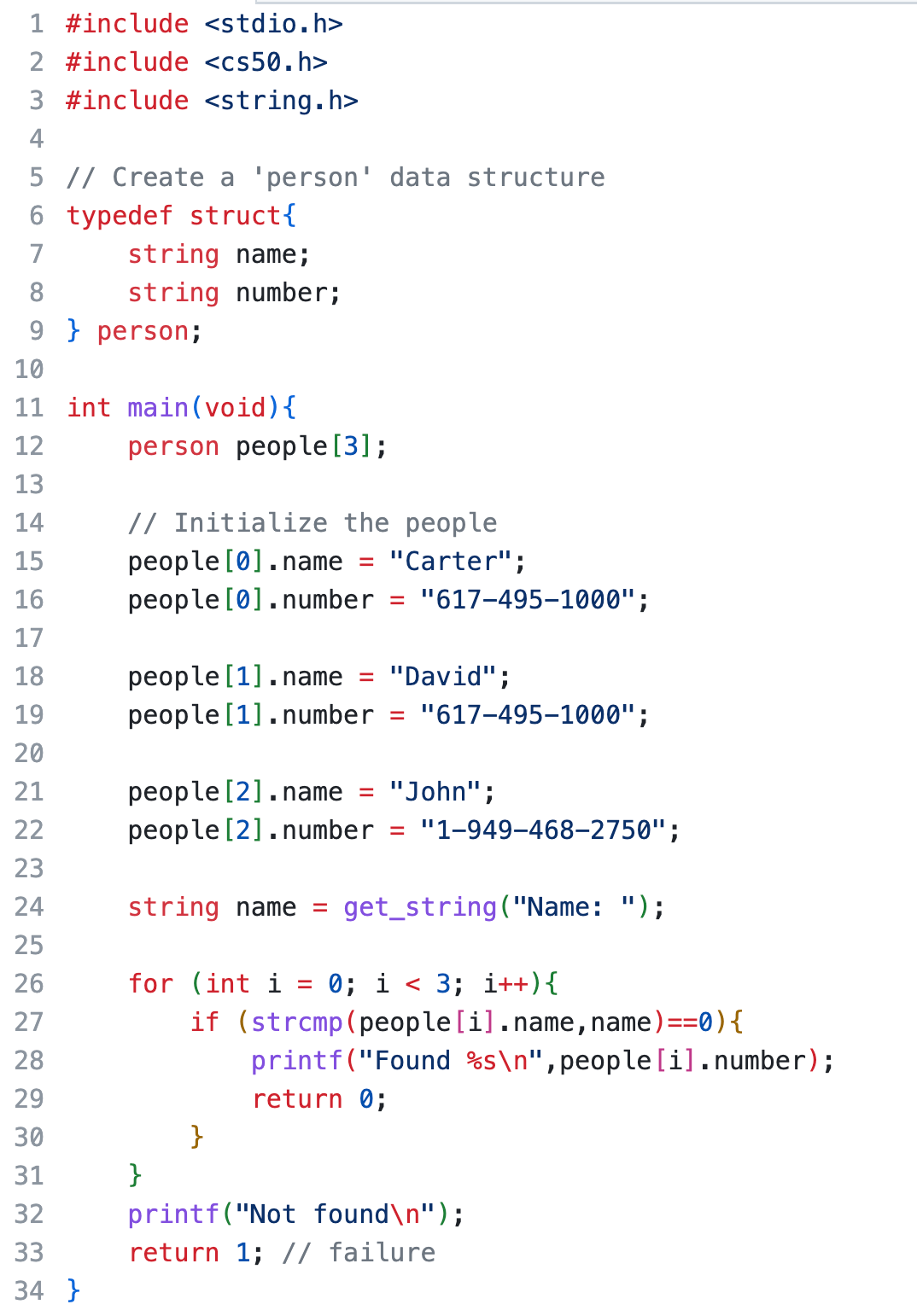

Sorting

Since it's much faster to search for a list of sorted data, how can the computer actually sort data?

What if you have a series of numbers: 7 2 5 4 1 6 0 3 and you want to sort this.

Selection Sort

You check every number one at a time and with every number you ask yourself "is this the lowest number".

• So you start with 7. Is this the lowest number? Yes, because it's the first number you've checked. This is the lowest number at this time. You store it somewhere in a variable.
• You proceed with 2. This is smaller, so you replace the value of the variable with 2.
• You proceed with 5. It's now lower, so skip.
• You proceed with 4. It's not lower, so skip.
• You proceed with 1. It's lower, so replace the value of the variable with 1.
• You proceed with 6. It's not lower, so skip.
• You proceed with 0. It's lower, so replace the value of the variable with 0.
• You proceed with 3. It's not lower, so skip.
• End of the data

So now you know that the lowest number is 0, but where do you put it? You can't just add it somewhere, but you can swap it with 7. It wasn't on the right place anyway, so it wouldn't cause any issues.

Now you know that 0 is in the right spot, so you can 'cut' this part from the array.

You repeat the process, but now you start with 2. So you keep going through allt he digits, remember the lowest value and swap that value with the starting position.

The pseudo code would look like this

For i from 0 to n-1
  Find smallest number between numbers[i] and numbers[n-1]
  Swap smallest number with numbers[i]

Comparison Sorting Visualization

Formula

So the first time you do the check, you have to do it 7 times (there are 8 numers, but you compare the first one to all the others).

(n-1)

The second time you don't have to worry about the first item anymore since that's in the right position, so you know have to do the loop (n-2) times

So the whole process would look like this:

(n-1) + (n-2) + (n-3) + ... + 1

Or more compact

n(n-1)/2

(n²-n)/2

n²/2 - n/2

Resulting in this Big O Notation:

O(n²)

Why n²? Well, you have to look through all the numbers in the array n times. That's your first loop. Then, inside that loop you have another loop that checks if the current number is the lowest number it has encountered. So n².

What would the Omega be? Is there a "best case" here? Not really, because the loop will run the exact same way. It will look through every number.

Ω(n²)

And since they are the same:

Θ(n²)

Bubble Sort

Let's try something else. You look at every number and the number next to it. If they are out of order, you swap them. Now you end up with this array:

2 5 4 1 6 0 3 7

Now the last number is always at the right spot.

You repeat the proces.

2 4 1 5 0 3 6 7

Now the last 2 numbers are on the right spot.

You repeat the proces.

2 1 4 0 3 5 6 7

Now the last 3 numbers are in the right place

1 0 2 3 4 5 6 7

Now you only need to replace it one more time

0 1 2 3 4 5 6 7

The pseudo code would look like this:

Repeat n times 
  For i from 0 to n-2
    If numbers[i] and numbers[i+2] out of order 
      Swap them

Why do we use n-2 here and not n-1? Because we're taking a number and comparing it to the next one, so you can't compare the last element with something. You can only compare the second to last element of the array with the last element.

The formula looks like this:

(n-1) * (n-1)

n² - 1n - 1n + 1

n² - 2n + 1

When n gets really large, we don't really care about that +1 at the end or even the 2, because that'll only be a drop in the bucket if the n gets really large.

O(n²)

So the upper bound is "the same" (not really) as selection sort.

But we can make an improvement in our pseudo code, because we can abort our code early.

If we go through the array the first time and we don't have to swap anything, then we can conclude that the array is already ordered and we don't have to do any additional loops.

Repeat n times 
  For i from 0 to n-2
    If numbers[i] and numbers[i+2] out of order 
      Swap them
    If no swaps
      Quit

In the best case, we can get away with n steps (because you need to go through the array at least once).

Ω(n)

So there is no theta notion here, since the Big O Notation and Omega notation are different.

Comparison Sorting Visualization

Recursion

Both selection sort and bubble sort are pretty inefficient, especially when the n gets really large.

Recursion is a description for a function that calls itself.

Remember our pseudo code that we wrote to find the 50 dollar bill in the closed lockers (with sorted values). We go to the middle locker, check if the value we're looking for is on the left or right side, etc.

If no doors left
  Return false
If number behind middle door
  Return true
Else if number < middle door
  Search left half
Else if number > middle door
  Search right half

Here we use a 'search' keyword inside code that is already searching. Usually when we call a function in a function the function would you keep running forever, but not in this case. Because every time we run it, the problem is going to be cut in half. So when you have the base case (if no doors left; return false), you'll always terminate the program when the job is done.

In the phone book example, the recursion pseudo code would look like this:

Pick up phone book
Open to middle of phone book 
Look at page
If person is on page
  Call person
Else if person is earlier in book
  Search left half of book
Else if person is later in book
  Search right half of book
Else
  Quit

Even the Mario pyramid example was actually recursive.

• What is a pyramid of height 4? It's a pyramid of height 3 plus 1 row
• What is a pyramid of height 3? It's a pyramid of height 2 plus 1 row
• What is a pyramid of height 2? It's a pyramid of height 1 plus 1 row
• What is a pyramid of height 1? It's just a single brick (this is our base case)

If we want to print out a pyramid of a certain height (provided by the user), we can program it iterative like this:

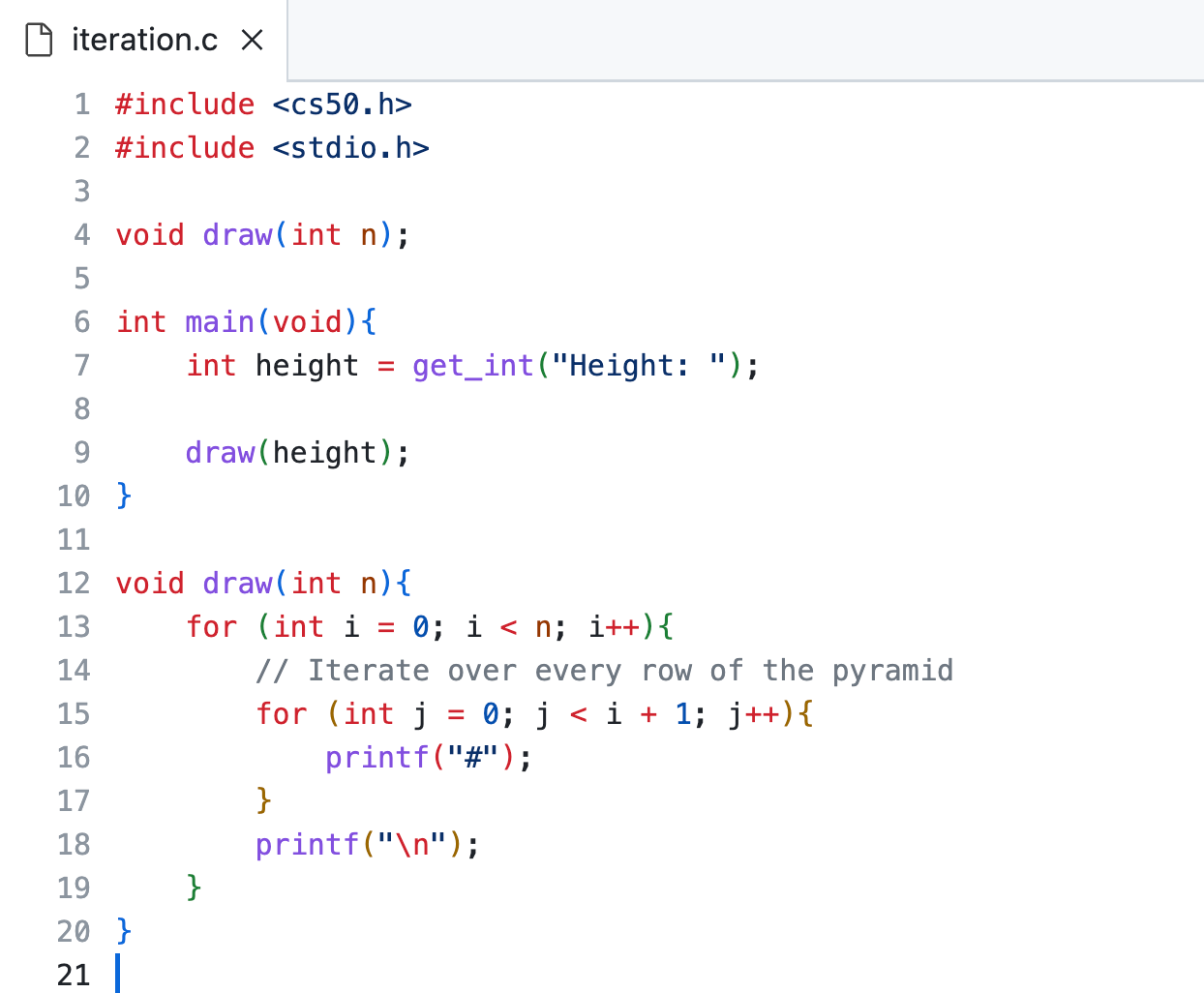
However, we can also program this in a recursive way.

So this is a bit hard to grasp, but let's think about what happens if you enter a height of 4.

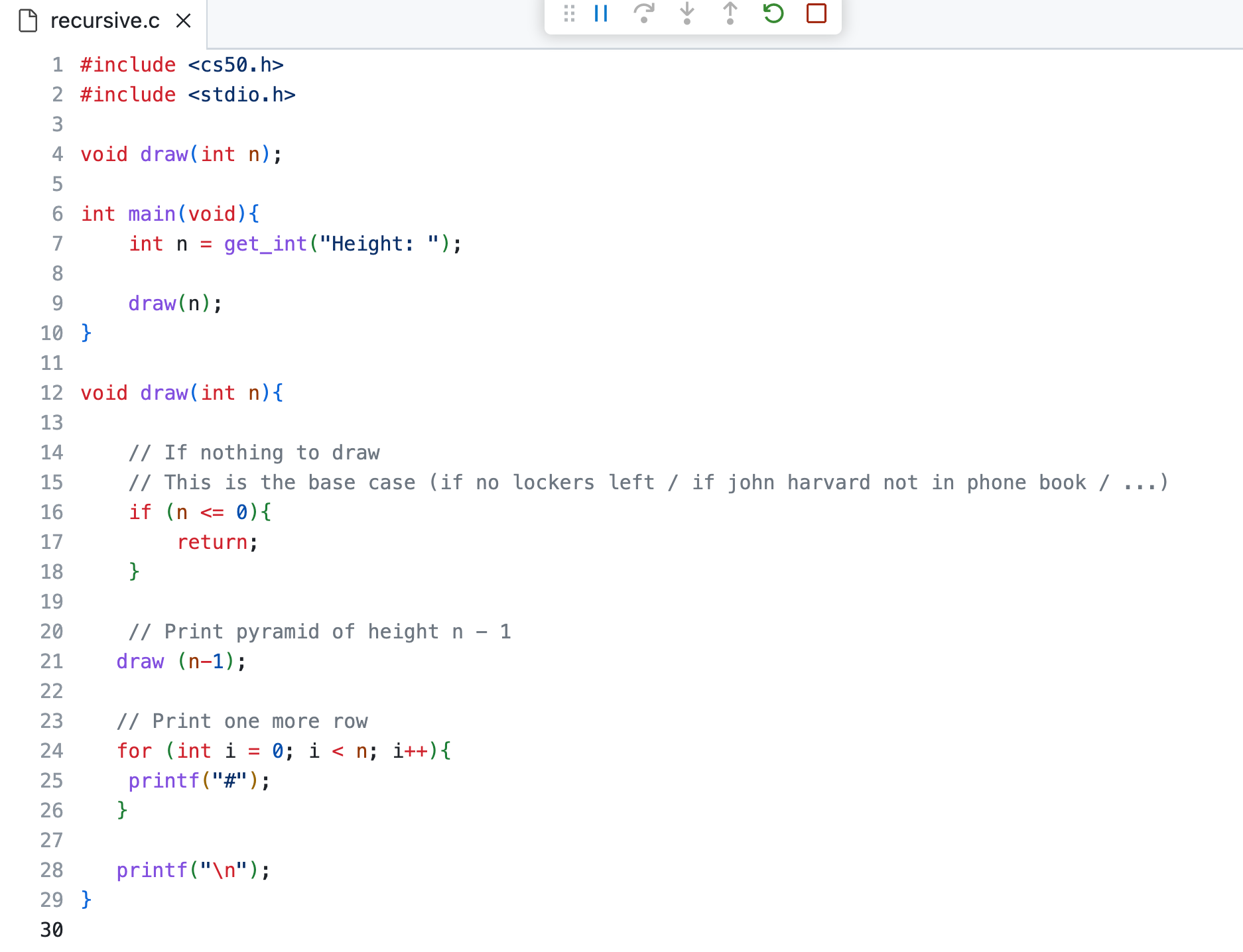
• The user enters '4', so 'n' is now 4
• The draw functions gets called with a parameter with a value of 4.
• It checks the if-condition, if 4 is not less or equal than 0, so it continues.
• It comes across the draw (n-1) line, so now the function gets called again. The important thing to understand here, is that the function that we were just in (the draw(4)) function doesn't get aborted. It just gets 'paused'.
• So we run the draw function again, this time with 3.
• We pass the if-statement
• We call draw(2), so we pause the current function call of draw(3)
• We pass the if-statement
• We call draw(1), so we pause the current function call of draw(2)
• We pass the if-statement
• We call draw(0), so we pause the current function call of draw(1)
• We DON'T pass the if-statement this time, because the value of our parameter is 0. So we exit this "instance" of the function.
• We return to the previous function call (which is draw(1)), and execute the rest of the code. So we print 1 brick and we print the new line.
• This function call is done now, so we proceed with the other function call that got 'paused'. Now we run draw(2), so we print 2 bricks and a new line
• Etc...

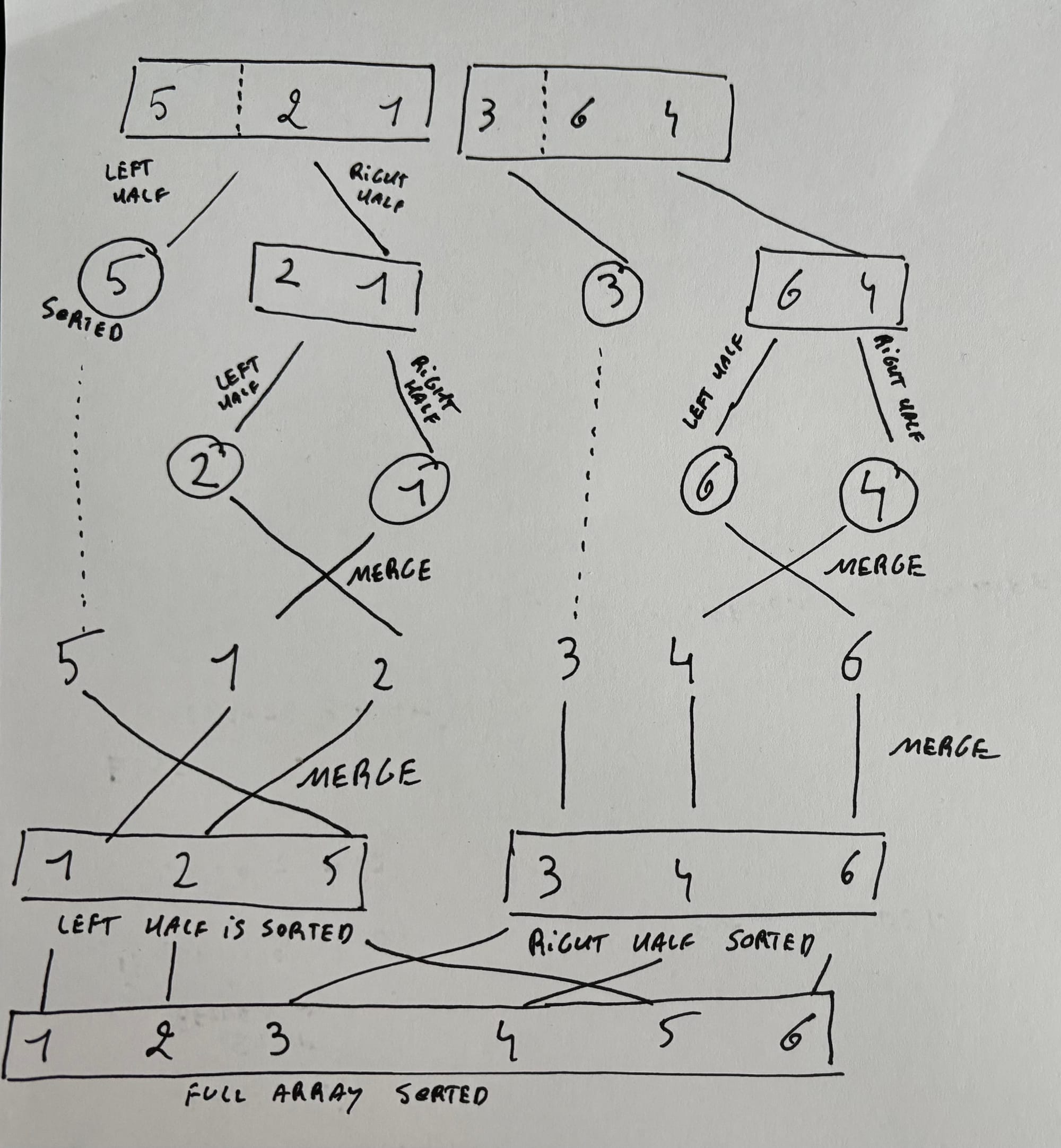
We can use this principle for a different kind of sorting method, namely Merge Sort.

Merge Sort

If only one number
  Quit
Else
  Sort left half of numbers
  Sort right half of numbers
  Merge sorted halves

So let's go back to the array of numbers:

6 3 4 1 5 2 7 0

Left half

We divide the set in half, and we put the left half in another array;

6 3 4 1

So how do we sort this? We recursively use the same algorithm. So we sort the left half of the left half.

We take 6 3 and put it in another array.

Same thing, we divide in half.

Now we have 1 array with 6, and 1 array with 3.

This is where we trigger the base case (if only 0ne number, quit) and continue to the other part of the algorithm: merge sorted halves. So we compare the 6 and the 3 and sort them. So now the list of size 2 is sorted.

We are now done finishing the left half of the left half.

Time to sort the right half of the left half.

Now we have an array of size 2 with 4 and 1.

We divide it in half again, so we have 4 and 1.

We compare, sort and now the right half of the left half is sorted.

Now that we have these two, we can merge these two together.

3 6 1 4

Becomes

1 3 4 6

We are now done finishing the left half.

Right half

Now we sort the right half

5 2 7 0 is an array of size 4.

We create an array of size 2 with 5 and 2.

This becomes two seperate arrays of 5 and 2 and we merge them

2 5

Now we sort the right half of the right half

We have an array of 7 and 0.

These become two seperate arrays of each one number: 7 and 0.

We merge them to get an array[2] of 0 7.

We merge the array of 2 5 with the array of 0 7 to get an array of size 4:

0 2 5 7

Merge

Now we have a sorted left half and a sorted right half:

1 3 4 6 0 2 5 7

We merge these two and it becomes

0 1 2 3 4 5 6 7

As you can see, this approach is way faster:

log2n refers to everything that we do in half (dividing dividing dividing). This is what we're doing here.

If we want to sort 8 numbers, we do

log(2) 8

Which is the same as

log(2) 2³

The base and the number cancel out, so that's actually 3.

log(2) of 8 is 3, which means that the total running time is

n log(2) n

Big O notation:

O(n log n)

It is also an omega of n log n

Ω(n log n)

Which means that sometimes bubble sort may outperform it when the outputs are already sorted.

Θ (n log n)

Shorts

Linear Search

Linear Search is an algorithm to find an element in an array.

You iterate from left to right and search for a specified element. If you find the element you're looking for, you stop. Otherwise, you move on to the next element.

If the item you're looking for is not in the array, you still have to go through the whole array to come to that conclusion.

Worst-Case Scenario

We have to look through the entire array of n elements, because the target element is the last element of the array or doesn't exist in the array at all.

O(n)

Best-Case Scenario

We find the element immediately because it's on the first place in the array.

Ω(1).

Binary Search

Unlike linear search, the array must first be sorted.

The idea of the algorithm is to divide and conquer, reducing the search array by half each time, trying to find a target number.

Pseudo code

Repeat until the array is of size 0
  Calculate the middle point of the current array 
  If the target is at the middle, stop. 
  Otherwise, if the target is less than what's at the middle, repeat, changing the end point to be just to the left of the middle. 
  Otherwise, if the target is greater than what's at the middle, repeat, changing the start point to be just to the right of the middle.

With every iteration, you get a new start point and end point for the (sub)array. When the end point and the start point are identical, the element is on the last place you were looking for. If they cross (the start point is higher than the end point), you know that the item you're looking for doesn not exist in the array.

Worst-Case Scenario

We have to divide a list of n elements in half repeatedly to find the target element, either because the target element will be found at the end of the last division or doesn't exist in the array at all.

O(log n)

Best-Case Scenario

The target element is at the midpoint of the full array, and so we can stop looking immediately after we start.

Ω(1)

Binary Search is a lot better than linear search, but you need to have a sorted array first.

Selection Sort

A computer doesn't have a birds eye view of an array, so it has to look at each element in the array seperately. So knowing that, how can the computer sort an array?

The computer looks at each number seperately, and with every iteration it asks itself "is this the lowest number that I've come across". If that's the case, it stores it in a temporary variable. When the iteration is done, it swaps the lowest number with the starting point of the array. Now we know that the first element of the array is sorted, and we don't have to consider that anymore.

We run the iteration again, but this time we start not from index 0, but from index 1.

This way, each iteration the array get's sorted from left to right, until you get to the end of the array.

Repeat until no unsorted elements remain: 
  Search the unsorted part of the data to find the smallest value
  Swap the smallest found value with the first element of the unsorted part

Worst case scenario

We have to iterate over each of the n elements of the array (to find the smalles unsorted element) and we must repeat this process n times, since only one element gets sorted on each pass.

O(n²)

Best case scenario

Even when the array is already fully sorted, we still have to go through the array n times and run the exact same process as the worst case scenario (although we won't have to make any swaps).

Ω(n²)

Bubble Sort

In Bubble Sort, you look at each adjacent pair in the array, and swap them to sort them. By repeating this proces for n times, you eventually get a sorted array. After the first iteration, the highest number will be on the right side of the array. On the second iteration, the second to highest number will be on the right side of the array, etc.

For the new iteration, we don't have to consider the last place in the array anymore, because we know that this is already sorted. So for the new iteration, we only need to check n-1 items. For the next iteration, only n-2 items, etc.

Pseudocode

Set swap counter to a non-zero value 
Repeat until the swap counter is 0: 
  Reset swap counter to 0 
  Look at each adjacent pair
    If two adjacent elements are not in order, swap them and add one to the swap counter

So we repeat this process until the swap counter is 0, which means that we didn't have to swap anything in this iteration, which means that the array is fully sorted.

Worst-Case scenario

The array is in completely reverse order, so we have to "bubble" each of the n elements all the way across the array, and since we can only fully bubble one element into position per pass, we must do this n times.

O(n²)

Best-Case scenario

The array is already fully sorted and we make no swaps on the first pass.

Ω(n)

Recursion

The definition of a recursive function is one that, as part of its execution, invokes itself.

It's similar to the factorial function in math (n!). You calculate it by multipying all of the positive integers less than or equal to n.

So 5 factorial is 5 * 4 * 3 * 2 * 1.

As programmers, we would define the factorial function as fact(n)

fact(1) = 1 
fact(2) = 2 * 1 
fact(3) = 3 * 2 * 1
fact(4) = 4 * 3 * 2 * 1
fact(5) = 5 * 4 * 3 * 2 * 1
...

So, can't we just say that fact(2) is just 2 times the factorial of 1.

And is fact(3) not simply 3 times the factorial of 2?

fact(1) = 1
fact(2) = 2 * fact(1)
fact(3) = 3 * fact(2)
fact(4) = 4 * fact(3)
fact(5) = 5 * fact(4)

So, that means...

fact(n) = n * fact(n-1)

With every recursive function, you need two things:

• The base case, which when triggered will terminate the recursive process ( otherwise you cause an infinite loop).
• The recursive case, which is where the recursion will actually take place. This is where the function will call itself. It won't call itself in exactly the same way it was called, it will be a slight variation that makes the problem that it's trying to solve a bit smaller.

So in our example, this would be the base case:

fact(1) = 1

So we need to stop our function when we get to 1.

int fact(int n){

  // Base case
  if (n -- 1){
    return 1;
  } else {
    return n * fact(n-1);
  }

  
}

This function is a lot neater (and sexier, according to Doug Lloyd) than this function that does exactly the same thing:

int fact2(int n){
  int product = 1;
  while(n > 0){
    product *= n;
    n--;
  }
  return product;
}

It's also possible to have multiple base cases. This would be the case (pun intended) with the Fibonacci number sequence. If n is 1, return 0. If n is 2, return 1.

You can also have multiple recursive cases, for example The Collatz conjecture.

Collatz conjecture

The collatz conjecture applies to positive integers and speculates that it is always possible to get "back to 1" if you follow these steps:

• if n is 1, stop (base case)
• Otherwise, if n is even, repeat this process on n/2.
• Otherwise, if n is odd, repeat this process on 3n + 1.

If you'd write a piece of software that counts the amount of steps needed to get to 1, it could look like this:

int collatz(int n){

  // Base case 
  if (n == 1)
      return 0;
  // Even numbers
  else if ((n%2) == 0)
      return 1 + collatz(n/2);
  // Odd numbers
  else
      return 1 + collatz(3*n+1);
}

Merge Sort

The idea is to sort smaller arrays and then combine those arrays together (merge them) in sorted order.

So instead of having one 6 element array, let's think about it as 6 arrays of 1 element arrays and just recombine them in a sorted order.

Pseudocode

Sort the left half of the array (assuming n > 1) 
Sort the right half of the array (assuming n > 1)
Merge the two halves together

Worst-case scenario

We have to split n elements up and then recombine them, effectively doubling the sorted subarrays as we build them up. (combining sorted 1-element arrays into 2-element arrays, combining sorted 2-element arrays into 4-element arrays...).

O(n log n)

Best-case scenario

The array is already perfectly sorted. But we still have to split and recombine it back together with this algorithm.

Ω(n log n)

In the best-case scenario it can be slower than bubble sort where the array is already perfectly sorted. But in the worst case (or average case), merge sort is going to be faster but is going to use more memory (because we create a lot of subarrays)